본격적으로 머신러닝 공부에 들어가기 전에, 확률에 대한 기초 배경지식을 리뷰할 필요가 있습니다. 기본적인 내용들은 아래 기존 글들을 참고하시면 될 것 같고, 이 글에서는 이산/연속 확률변수에 대하여, 결합확률분포(joint probability distribution), 주변확률분포(marginal probability distribution), 조건부 확률분포(conditional distribution)의 개념을 정리하고, 확률변수의 독립에 대해 간단히 살펴보려고 합니다.
1. 확률의 여러 개념들 병원에서의 어떤 대화 어떤 환자가 병원에 방문하여 생명을 구할지도 모를 약을 처...
blog.korea-iphone.com
이 글은 아래 글에 이어지는 확률기초 관련 내용 정리입니다. 1. 곱셈 법칙과 조건부 확률 (multiplication...
blog.korea-iphone.com
이 글은 아래 글에 이어지는 확률기초 관련 내용 정리입니다. 1. 독립(independence) 사건과 확률 <독립...
blog.korea-iphone.com
이 글은 표본공간(sample space), 확률변수(random varibles)를 안다고 가정하고 작성하였습니다. 확률분포...
blog.korea-iphone.com
이산확률변수(discrete random variable)의 결합/주변/조건부 확률분포
결합확률분포(joint probability distribution) 및 결합확률질량함수
결합확률분포는 두 개의 서로 다른 확률변수(예를 들어, X, Y)가 있을 때, 이 두가지 확률변수가 '동시에' 일어날 때의 확률분포를 의미합니다. 다시 말해, 단일 변수인 경우 확률변수 X가 x라는 값을 가질 때의 확률을 P(X=x)라고 하고, 확률변수 Y가 y라는 값을 가질 때의 확률을 P(X=y)라 하면, 결합확률분포는 X = x, Y = y가 동시에 일어나는 경우의 확률이 결합확률이 되며, P(X = x, Y = y)라고 쓸 수 있습니다. 이경우, 결합확률질량함수(Joint probability mass function) pX,Y(x,y) 는 다음과 같이 쓸 수 있습니다.
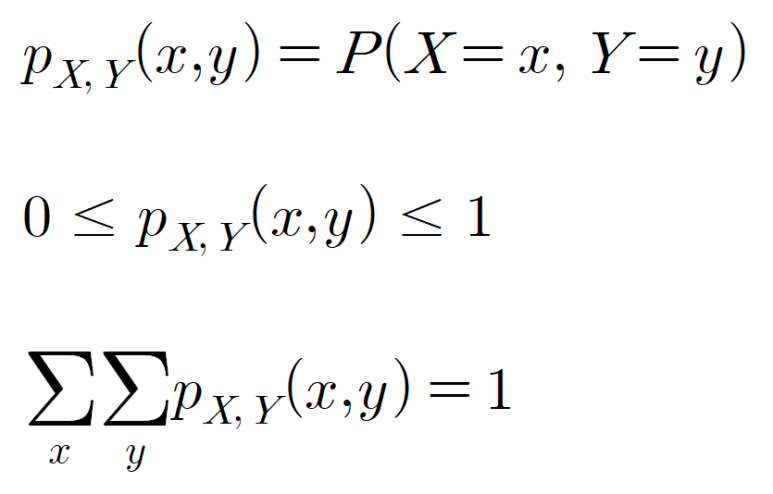
간단히 두 개의 확률변수로 이뤄진 예를 들어봅니다. 아래 표에서 확률변수 X는 시험준비를 위해 공부한 시간, Y는 점수 분포를 의미합니다.
*아래 표의 수치들은 Kahn Academy에서 가져와(), 제가 새로 작성/보완한 것입니다.
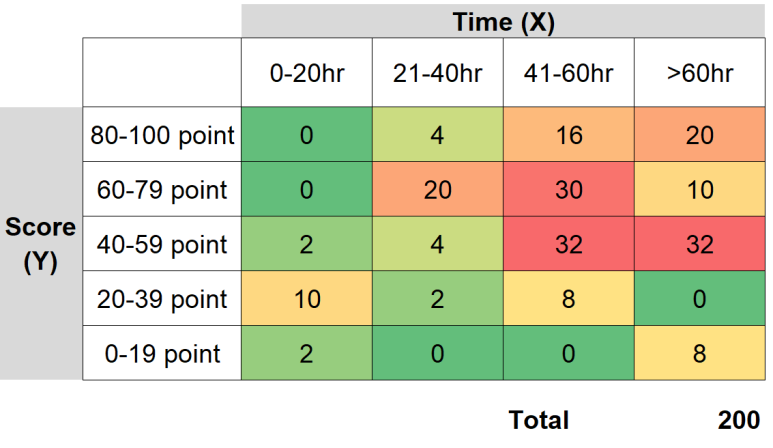
<공부 시간과 점수 관계: raw data (단위: 명)>
위 내용을 확률로 나타내면 아래 그림과 같습니다. 예를 들어, 21-40시간을 공부한 학생이 60-79점을 맞을 확률은 0.1(10%)입니다. 이와 같이, 두 확률변수에 대하여 특정 이벤트가 동시에 일어나는 경우의 확률을 나타낸 것이 결합확률이 됩니다. 그리고 이산확률분포의 확률밀도함수(PMF)와 마찬가지로 모든 P(X=x, Y=y)는 각각 0보다 크며, 그 전체의 합은 1이 됩니다.
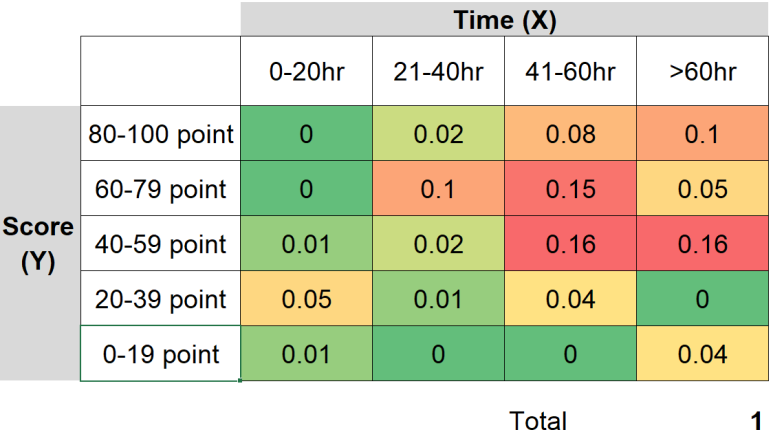
<공부 시간과 점수의 관계: 결합확률 P(X=x, Y=y)들>
주변확률분포(marginal probability distribution)
주변확률분포는 앞서 보여드린 X, Y의 결합확률분포로부터, X만의 확률분포 또는 Y만의 확률분포를 구하는 것입니다. 이 때, 확률변수 X의 주변확률분포는 각각의 X값 범위(0-20, 21-40, 41-60, 60이상)에 속한 모든 Y를 합치면 됩니다. 마찬가지로, 확률변수 Y의 주변확률분포는 각각의 Y값의 범위(0-19, 20-39, 40-59, 60-79, 80-100)에 속한 X들을 모두 더하면 됩니다. 각각의 주변확률분포 역시 다른 확률분포처럼 그 합은 1이 되어야 합니다.
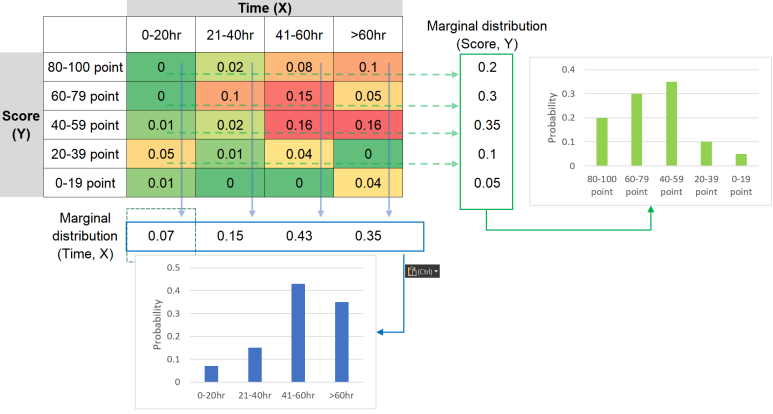
<이산확률변수의 주변확률분포>
위에서 말로 설명한 것을 식으로 표현하면 아래와 같습니다. pX(x)는 확률변수 X의 주변확률질량함수(Joint probability mass function), pY(y)는 확률변수 Y의 주변확률질량함수를 의미합니다.
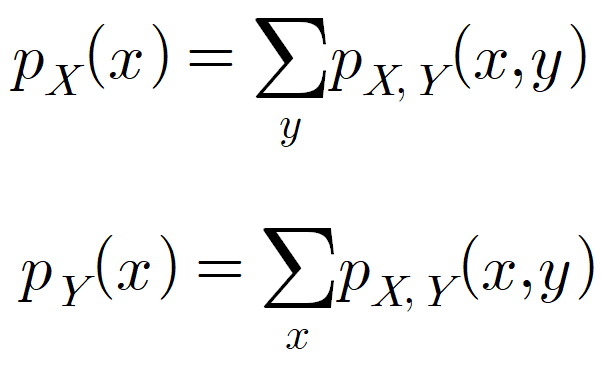
조건부 확률분포(conditional distribution)
조건부확률분포는 X, Y 두 확률변수중에 하나(예를 들어, X)의 값이 주어졌다(고정되었다)고 생각하고, 그 때의 또다른 확률변수(Y)의 확률분포를 구하는 것입니다. 아래 그림에서, 만약 우리가 확률변수 Y가 40-59점일 때의 확률변수 X의 조건부 확률분포는 아래와 같이 찾을 수 있습니다. 이 때, 유의할 것은 조건부 확률분포 역시 그 합이 1이어야 하므로, 40-59점일에 해당하는 전체 확률 0.35로 각각의 확률을 나누어 주어 그 합이 1이 되도록 만들어 준다는 점입니다.
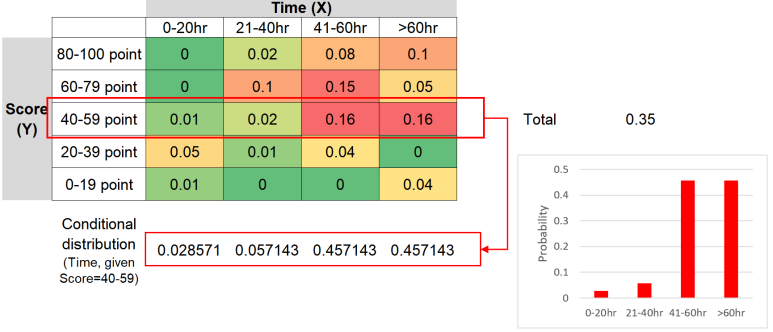
<이산확률변수의 조건부 확률분포>
위에서 말로 설명한 조건부 확률질량함수(conditional probability mass function)는 아래와 같습니다.
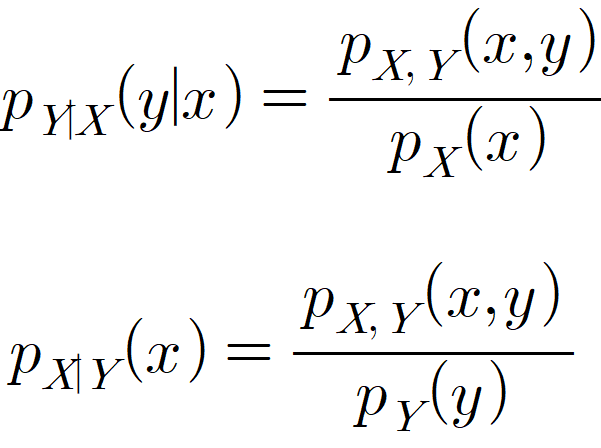
연속확률변수(continuous random variable)의 결합/주변/조건부 확률분포
연속확률변수의 결합, 주변, 조건부 확률분포의 기본적인 개념은 앞서 설명드린 이산확률변수의 경우와 같습니다. 다만, 결합확률분포가 확률질량함수(PMF)가 아니라, 연속된 함수인 확률밀도함수(PDF)로 나타난다는 점이 다르죠. 그리고 확률질량함수와는 달리, 확률밀도함수에서는 어떤 하나의 점(X=x 이고 Y=y인 하나의 point)에 대한 확률은 계산되지 않습니다. 앞서, 확률 기초 부분에서 살펴보았듯, 연속확률변수의 확률은 확률변수의 어떤 구간에 속할 확률(즉, 적분)로서 나타낼 수 있겠죠.
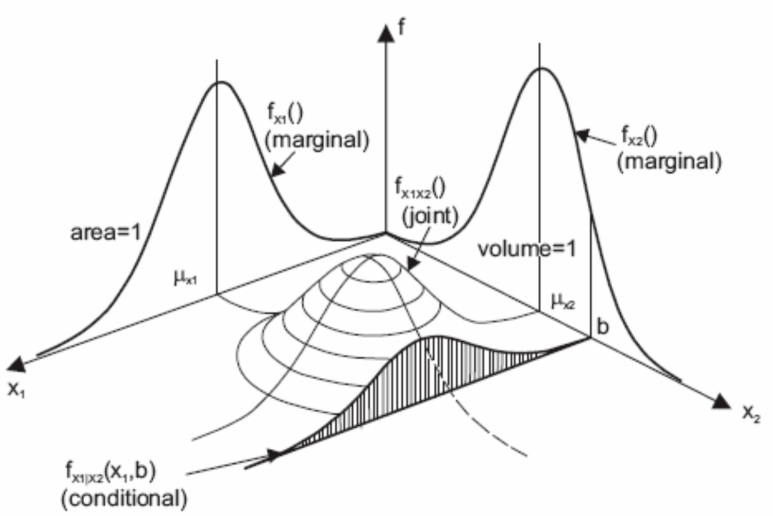
<결합확률분포와 주변확률분포, 조건부 확률분포 개념, *출처: Melchers (1999)>
결합확률분포 및 결합확률밀도함수(joint probability density function)
결합확률분포의 x,y지점의 누적확률분포함수 FX,Y(x,y)는 아래와 같이 나타낼 수 있습니다.
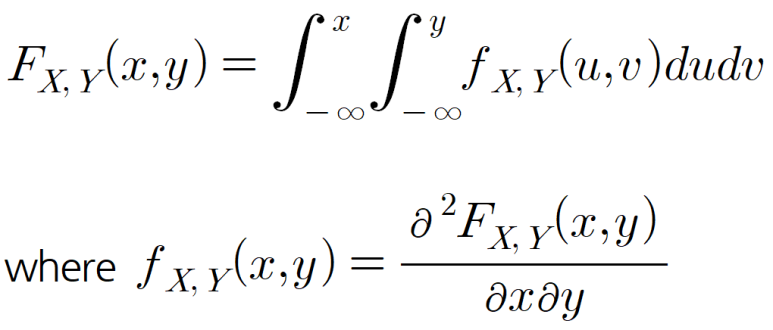
또한, 결합확률밀도함수를 fX,Y(x,y)라 하면, 아래와 같은 성질을 갖습니다. 즉, 모든 확률분포값은 0보다 크고, 그 전체를 적분하면 1이 됩니다. 확률분포의 기본적인 성질이죠.
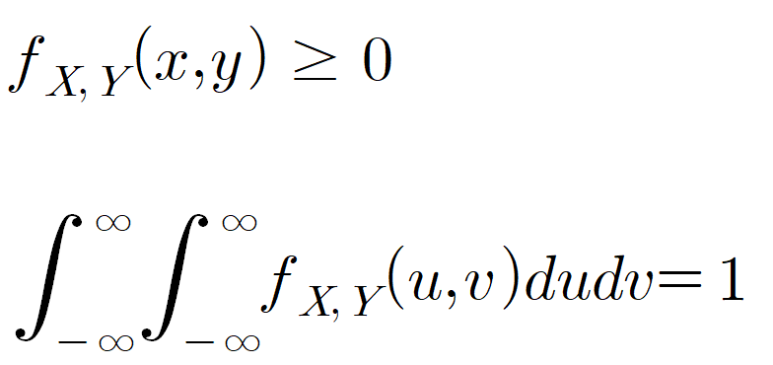
그리고 확률변수 X,Y의 일정한 영역을 A에 속할 확률은 다음과 같이 계산됩니다.
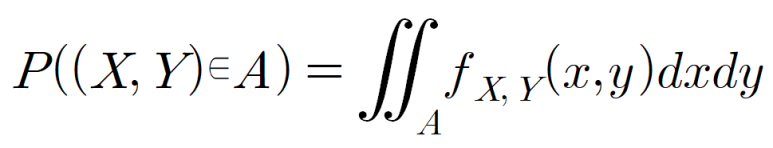
위와 같은 내용을 좀 더 구체화하여 풀어쓰면 아래와 같은 의미입니다.
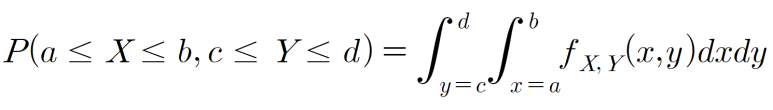
주변확률분포 및 주변확률밀도함수(marginal probability density function)
이산확률분포의 경우와 비슷한 개념이지만, 연속(continuous) 함수이기 때문에 ∑가 아니라, 적분이 됩니다. 즉, 확률변수 X의 주변확률분포를 구할 때는 결합확률밀도함수를 Y에 대하여 적분하고, 확률변수 Y의 주변확률분포를 구할 때는 결합확률밀도함수를 X에 대하여 적분하면 됩니다.
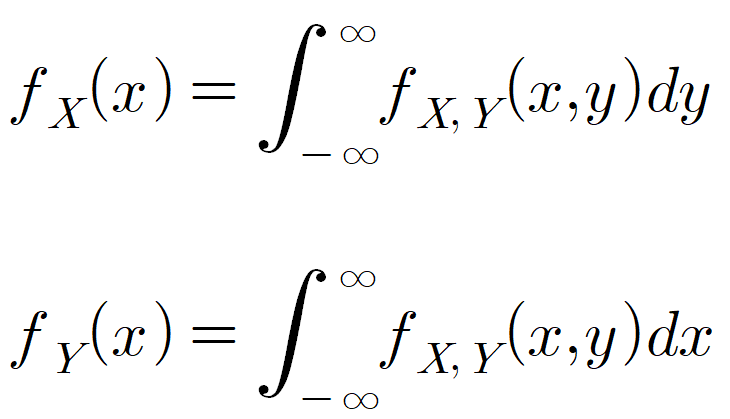
조건부 확률분포
아래 애니메이션은 확률변수 X가 특정한 값으로 주어졌을 때, 확률변수 Y의 조건부 확률값이 어떻게 변화하는지를 시각적으로 표현한 것입니다. 이 경우, 마지막에 파란색으로 위로 볼록하게 표현된 평면이 바로 X, Y의 결합확률밀도함수를 의미하게 되겠죠.
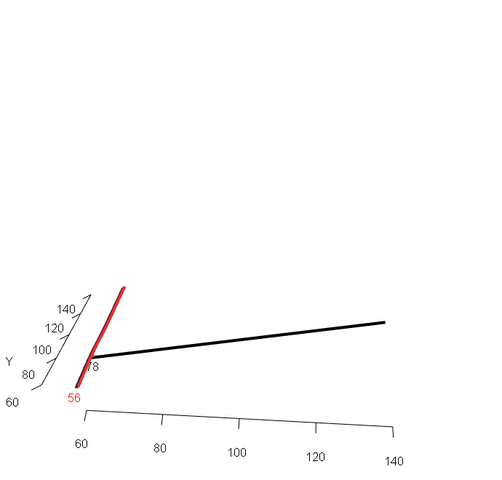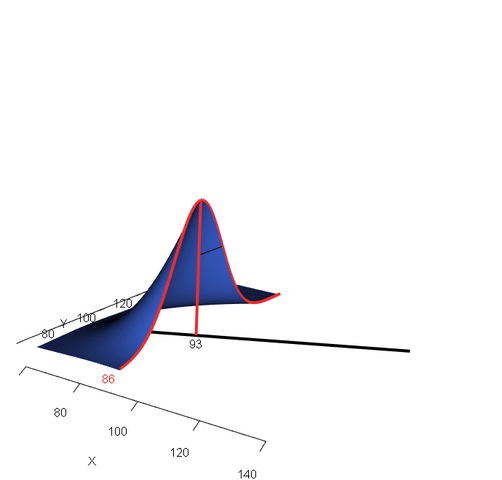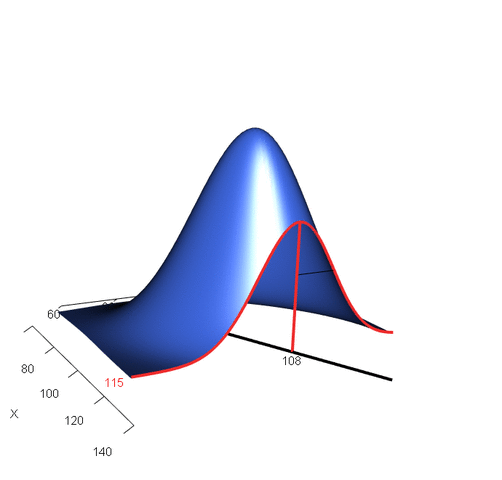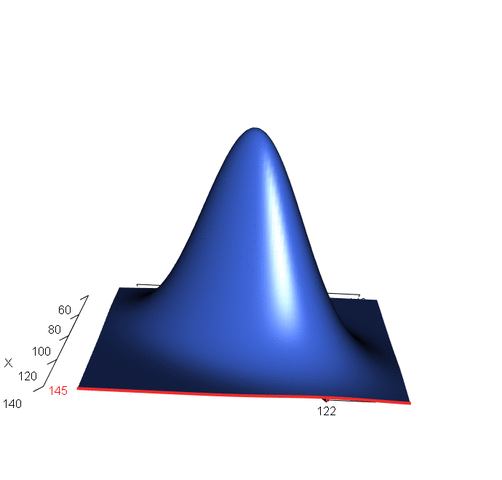
<조건부 확률 분포(conditional distribution)의 시각화, 출처: >
연속확률변수에 대한 조건부 확률분포는 이산확률변수와 비슷하게 아래와 같이 식으로 표현할 수 있습니다. 마찬가지로, 해당하는 조건의 결합확률밀도함수값을 주변확률밀도 함수값으로 나누어, 조건부 확률밀도함수의 적분값이 1이 되도록 해주어야 합니다.
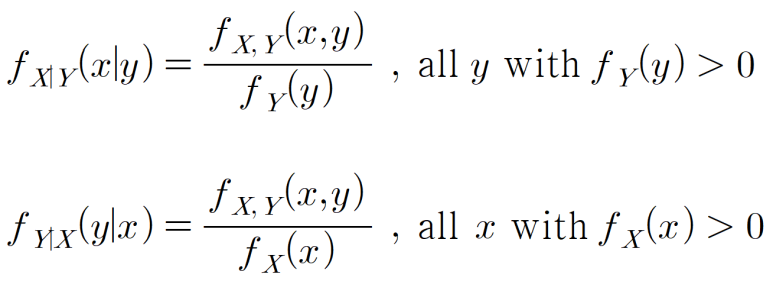
확률변수의 독립(independence)
이산확률변수를 예로 들면, 두 확률변수가 독립이면 다음이 성립합니다. 직관적으로 당연한 결과입니다. 두 확률변수가 독립이므로 y가 조건으로 주어졌을 때, x의 확률은 그냥 x의 확률과 같습니다.
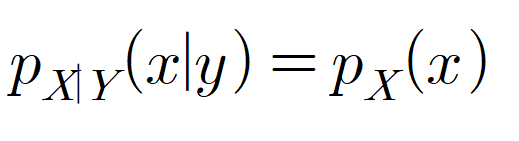
마찬가지로 X, Y가 독립이면, 아래와 같이 두 확률변수의 결합확률 pX,Y(x,y)는 각각의 주변확률분포의 해당 사건에 대한 확률값 pX(x), PY(y) 곱과 같습니다. 반대로, 이 각각의 확률의 곱이 결합확률과 같지 않으면, 두 확률변수는 독립이 아니라고 할 수 있습니다.
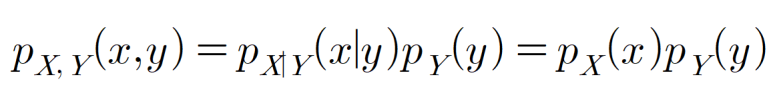
앞에서 예로 든 자료를 다시 보겠습니다. 여기서 공부시간(X)과 점수(Y)는 서로 독립일까요?

<공부 시간과 점수의 관계: 결합확률 P(X=x, Y=y)들>
앞서 말씀드린 독립 조건을 고려하여, 하나의 예를 들어 계산해 보면, 이 결합확률분포에서 X와 Y는 독립이 아니라는 것을 알 수 있습니다. 다시 말해, 둘 사이에는 상관관계가 있다는 얘기죠. 만약, 이 데이터가 실제라면 상식적으로, 더 많은 시간 공부한 사람이 더 좋은 성적을 얻을 것이므로 둘 사이에 상관관계가 있다고 볼 수 있을 겁니다. 어쨌든, 우리가 X,Y가 뭘 뜻하는지 모른다해도, 우리는 위와 같은 관계를 확인함으로써 두 확률변수의 독립 여부를 판단할 수 있습니다.
다음에 이야기 하게 될, 최대가능도추정(MLE, Maximum Likelihood Estimation)에서 파라미터를 추정할 때, i.i.d.를 가정하므로, 주어진(측정된) 값들이 실제로 서로 독립인지를 확인할 필요가 있게 됩니다.
[당부 말씀]
※ 저 역시 아직 끝없는 배움의 과정에 있기 때문에, 제 글에 오류 또는 착오가 있을 경우 지적해 주시면 감사하겠습니다.
※ 이 분야에 대한 정확한 내용이 필요하시면, 각종 교재나 논문 등 확실한 출처가 있는 자료를 활용하시기를 추천드립니다.